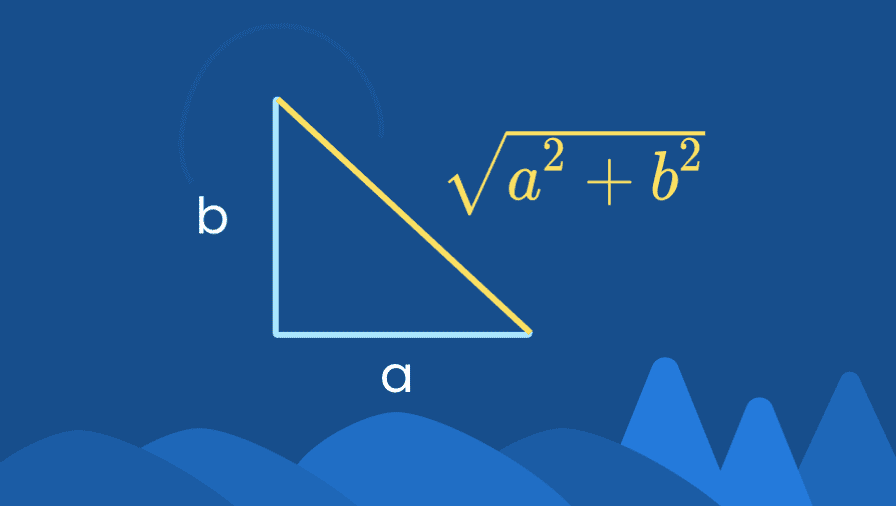Firstly, let me say that Pythagoras’ Theorem is a whole lot easier than it looks. In fact, once you have the formula down pat, you’re pretty much already there.
The purpose of the formula is to help us relate the three sides of a right-angled triangle however, you could find real world uses for the theorem in areas such as architecture and construction.
Formula
$$a^2 + b^2 = c^2$$
Here each letter represents a length of a side. For instance, a might be 5cm, b may be 12cm and c could be 13cm.
c is the longest side of the right angled triangle.
Idea
Our triangle has lengths a, b and c. If we make squares on each side of that triangle then something really cool happens:
The areas of the yellow and blue squares sum to give us the area of the green square.
If you were wondering how we calculated the area of each square:
Common Example
The most common kind of question will ask you to use the formula to find the longest side of the triangle.
For example, let’s find c on this triangle of this triangle:
We can let a = 3 and b = 4 in our formula – then all we will need to do is solve for c.
$$a^2 + b^2 = c^2$$
$$ 3^2 + 4^2 = c^2 $$
$$ \implies 25 = c^2$$
$$ \implies c = \sqrt{25} $$
$$ \implies c = 5 $$